交流电气装置的接地设计规范 GB/T50065-2011-环安宝@法规宝

        B．0．1  本规范中式(B．0．1-1)和(B．0．1-2)是参照《交流电气装置的接地》DL／T 621—1997的附录B的B1的式(B1)和(B2)引入的。但要注意规范中的分流系数定义与《交流电气装置的接地》DL／T 621—1997中的分流系数定义是不同的。

        B．0．2  在发电厂或变电站内、线路上发生接地故障时，线路上出现接地故障电流。故障电流经地线、杆塔分流后，剩余部分通过发电厂和变电站的接地网流入大地。这部分电流即为接地网的入地接地故障电流I_g。而经接地网入地的计及直流偏移分量的接地故障不对称电流有效值I_G按下式计算：

I

        _G ＝D_f×I_g(12)

        式中：D_f——衰减系数。

        I_g与接地故障接地对称电流I_f的比值，称为故障电流分流系数S_f。

        故障电流分流系数包括站内接地故障和站外接地故障两种情况。相应的简化计算公式参见本规范附录B的公式(B．0．2-11)和(B．0．2-14)。这些公式参照解广润编写的《电力系统接地技术》(水利电力出版社，1991．5)给出。

        分流系数受导线、架空线路地线的布置、地线尺寸与材质、厂或站接地网与线路杆塔的接地电阻等多种因素的影响，在工程设计中宜采用专用计算分析程序对其专门加以计算。以下给出一个应用清华大学开发的接地计算分析程序获得的分流系数数值计算示例。

        分析所用模型如图11所示。该110kV输变电系统，两个变电站通过架空线路相连。线路采用如图12所示的SZ—16．4杆塔。相导线采用LGJ—240，地线采用GJ—50。杆塔接地电阻为10Ω。变电站B接地电阻为0．2Ω。两变电站相距7km，送电线路杆塔挡距为350m。变电站A内部发生单相接地故障。 

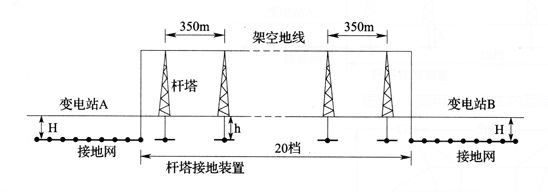
        图11 变电站A发生内部接地故障 

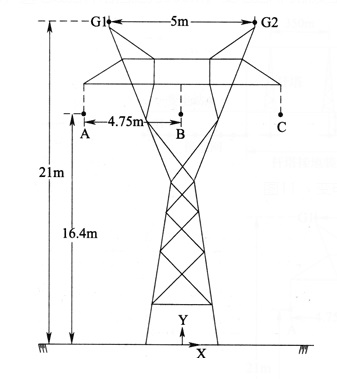
        图12 典型110kV型杆SZ-16．4

        表4～表9给出变电站接地电阻、杆塔接地电阻、不同地线材质、不同进出线回数及线路挡距长度等对分流系数影响的计算结果。这一示例显示，只有采用专门的计算机程序，通过数值计算才能使入地电流等的计算获得较为接近实际的结果，进而为设计选择出较为合理的方案。 

        表4 不同杆塔接地电阻时的分流系数 

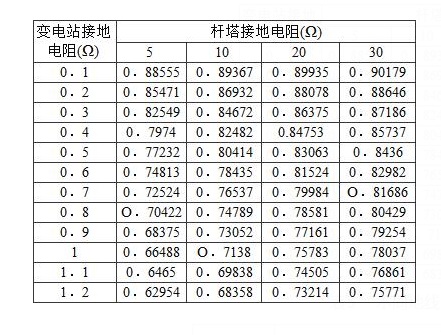
        表5 不同地线时的分流系数 

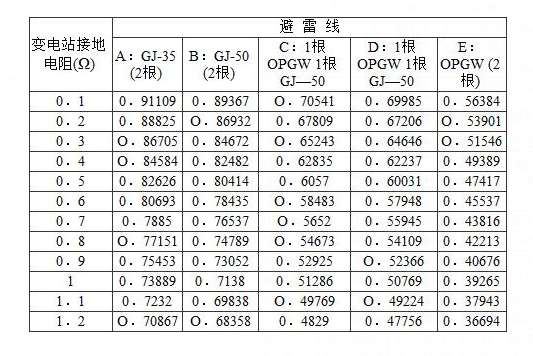
        表6 不同进出线回数对应的分流系数 

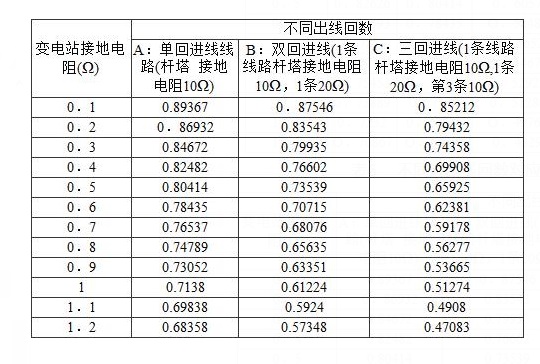
        表7 不同线路挡距长度的分流系数 

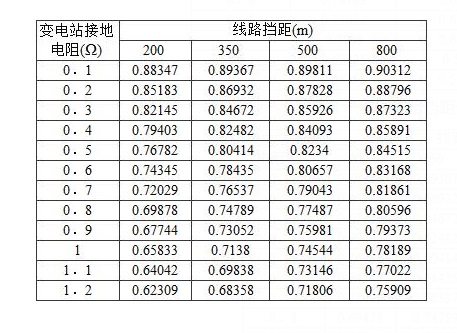
        表8 不同线路挡数的分流系数 

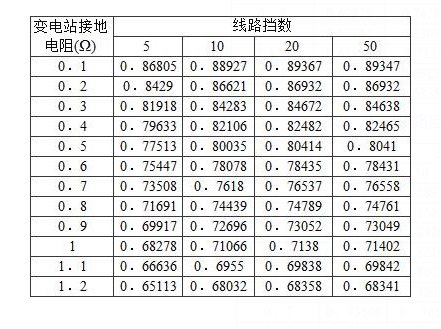
        表9 不同系统阻抗的分流系数 

        B．0．3  本规范中故障电流衰减系数D_f的计算公式引自《交流变电站接地安全导则》IEEE Std80—2000的15．10。

        《交流变电站接地安全导则》IEEE std80—2000中采用Dalziel的实验结论，确定人体安全电流与作用时间的关系为I²·t＝常数。在2005年出版的IEC 60479—1中，该关系近似为I^1.8·t＝常数。可见，电流对人体的作用大小主要取决于电流在人体内产生的能量。同样，这一能量中包含直流衰减分量的贡献，因此从人身安全的角度，应计及入地故障电流的直流分量。

        在故障电流流散到土壤的过程中，电流会产生与其幅值成正比的电磁力和与其幅值平方成正比的能量，有可能超越导体的热稳定容量，导致接地网导体的热熔和弯曲。入地电流的直流偏移分量对接地体承受的电磁力和吸纳的能量具有一部分贡献，因此从接地体安全的角度，也应计及入地电流直流分量的影响。

        从上述可得出结论，在设计接地网时，应计及故障电流直流分量的影响，按照接地网入地的最大接地故障不对称电流有效值I_G进行设计。

        下面介绍D_f的计算方法。

        如图13所示，接地网入地最大接地故障不对称电流有效值I_G是从接地网流入周围土壤中的最大非对称交流电流，它包括对称交流电流i_AC(图13中的a)及直流分量i_DC(图13中的b)。直流偏移是指电力系统暂态情况时，对称电流波和实际电流波之间的差值。实际的电流波采用数学的方法可以分解为两部分，对称的交流分量和单向的直流分量，直流分量随时间逐渐衰减，单向分量可以是正极性或负极性，但不能改变极性。直流偏移分量为故障电流峰值与对称分量的峰值的差值。直流分量一般称为直流偏移电流，随时间呈指数衰减。因为在设计接地系统时必须考虑非对称电流，因此为了考虑到在故障的开始几个周波内，由于直流分量的作用而产生的非对称故障电流波形，应考虑衰减系数D_f。

        一般，非对称的故障电流包括次暂态、暂态和稳态交流分量，及直流偏移电流分量。次暂态电抗是指故障起始时发电机的电抗，该值用于计算起始的对称故障电流。电流持续减小，但在计算时假设该电流在故障突然出现后稳定维持约0．05s。次暂态、暂态交流分量和直流偏移电流分量呈指数衰减，衰减速度各自不同。然而，为了简单起见，假设交流分量不随时间而衰减，保持其起始值。因此非对称故障电流是时间的周期函数，可以表示为：

        i_f(t)＝(√2UY)[sin(ωt＋α－θ)-exp(－t／T_a)sin(α－θ)] (13)

        式中：U——故障前相对中性点的标称电压；

        ω——系统角频率；

        α——电流起始时的电压相位角；

        θ——电流相位角；

        Y——交流系统等效导纳；

        Ta——直流偏移分量的时间常数，T_a＝X／(ωR)；

        X／R——对于给定的故障类型在故障位置处系统的X／R之比。系统次态故障阻抗的X和R分量用于确定X／R之比。 

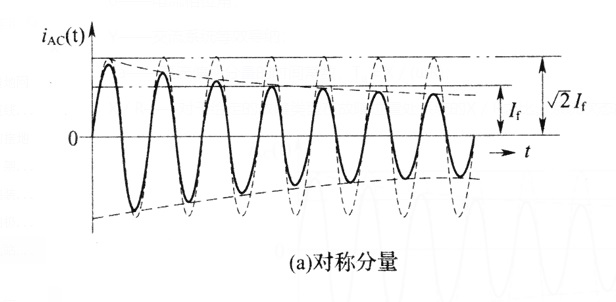
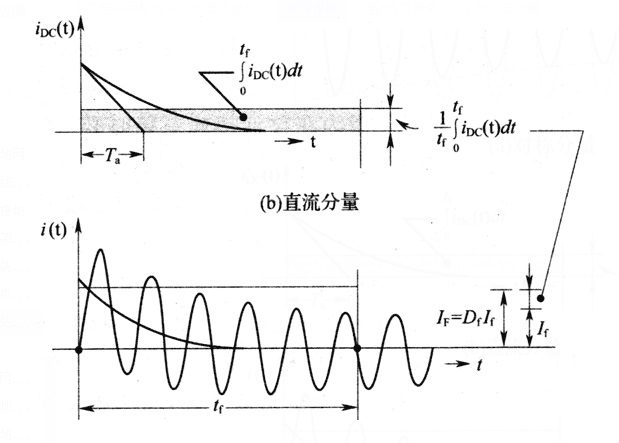
        (c)最大入地故障电流 

        图13 接地网最大入地故障电流(c)的对称分量(a)和直流分量(b)

        最严重的情况为α－θ＝－π/2时，直流偏移分量处于最大值。式(13)变为：

        i_f(t)＝(√2UY)[exp(－t／T_a)－cos(ωt)] (14)

        因为电击对于人心脏纤维性颤动的试验数据是基于常数幅值的对称正弦波的能量值确定的，因此对于非对称电流波，应根据其可能的电击暴露的最大时间来确定其等效有效值。根据有效非对称故障电流的定义，这个有效值I_F可以根据下列公式确定：

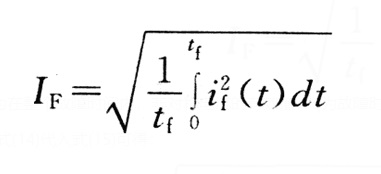        (15)

        I_F为在整个故障时间内，非对称电流的有效值；t_f为故障时间。

        将式(14)代入式(15)可得：

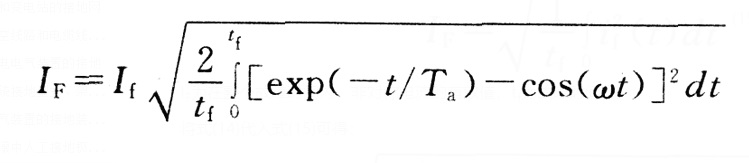(16)

        因此衰减系数D_f定义为I_F与／I_f的比值：

        D_f＝I_F／I_f (17)

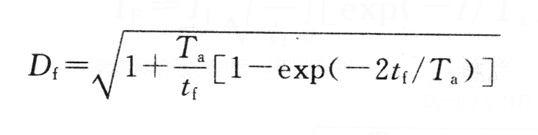        (18)

        本规范中表B．0．3就是通过式(18)的计算得到的。

        B．0．4  本规范中式(B．0．4)系引自《交流电气装置的接地》DL／T 621—1997附录C的式(C3)。但注意电流I_G为接地网入地的接地故障最大不对称电流有效值。